2.1 - Intro to Limits
Definition of a limit
- The value that a function approaches as the input approaches some value.
- A limit is different to a function value.
- Limits: all about approaching a value
- Pronounced “the limit as x approaches 2 of
is 5”
- Pronounced “the limit as x approaches 2 of
- Function values: are evaluated at a point
- Partial limits show what side a limit comes from.
comes from the left comes from the right - Partial limits always exist.
- Limits: all about approaching a value
Whether or not a limit exists
- For a limit to exist at
, the limit from the left side must equal the limit from the right side. - In algebraic terms, the
must equal . - Otherwise the limit does not exist (DNE)
- Use DNE when the right and left hand limits are not equal to each other. This includes things like vertical asymptotes for things like rational functions.
- Very rarely, use no limit for things that don’t even have a right/left hand limit.
Example of a limit not existing:
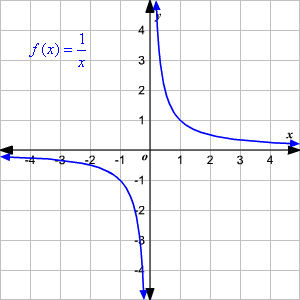
- In algebraic terms, the
Finding limits algebraically
Strategies:
- Direct substitution: just plug the limit into the function. Sometimes this doesn’t work because you get
. - Other strategies:
- Factoring
- Expanding
- Rationalizing
- Finding a common denominator
- Multiplying by a conjugate
- The big guns - L'Hopital's Rule
Limit of
An important fact that gets used a lot in these types of problems is the fact that
- This can be used in a variety of creative ways.
Average and instantaneous rates of change
- Average rates of change don’t require limits. They are just slope, and slope is calculated with two points.
- Instantaneous rates of change do, because you just have one point to work with.
Example
An object dropped from rest from the top of a tall building falls
Solution: Try using the points
- when
, - when
,
Now calculate the slope using these two points, using the limit as h goes to 0:
Solve this and eventually plug in(after cancelling the on the bottom) for a final answer of 128 ft/sec.