3.9 - Exponential and Log Derivatives

Now we can take the derivative of pretty much anything.

Derivative of $e^x$

• The derivative of $e^x$ is simply $e^x$.

Proof:

Derivative of any general $e^u$

${\displaystyle \frac{d}{dx}(e^u)=e^u\left(\frac{du}{dx}\right)}$

• This is the same as above – just chain it with whatever is in the exponent.

Derivative of any general $a^u$

• We use the fact that ${\displaystyle a^x=e^{\ln (a^x)}}$.
  ${\displaystyle \frac{d}{dx}(a^u)=a^u\ln a\left(\frac{du}{dx}\right)}$

Proof:

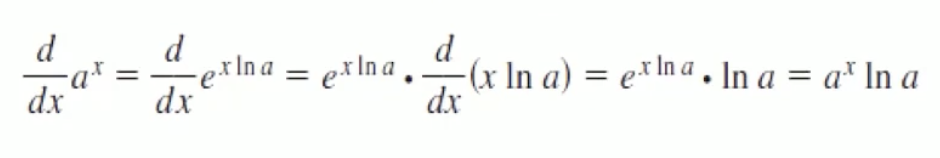
Derivative of $\ln x$

• Simply ${\displaystyle \frac{1}{x}}$.

Proof:

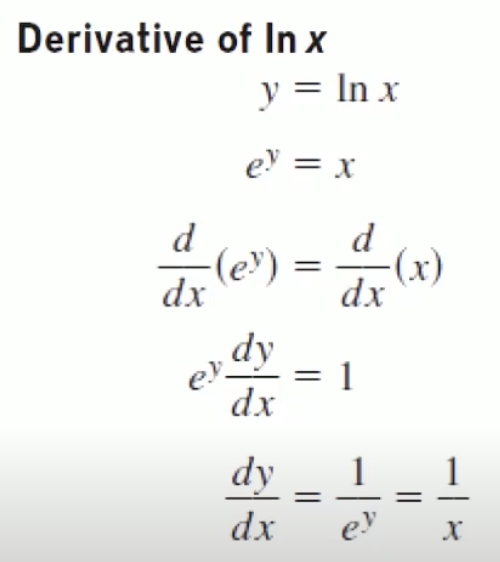
Derivative of any general $\ln u$

• Do the same as we did before – simply chain with the $u$ inside.
  ${\displaystyle \frac{d}{dx}(\ln u)=\frac{1}{u}\left(\frac{du}{dx}\right)}$

Derivative of ${\log }_{a}x$

• The derivative of ${\log }_{a}x$ is ${\displaystyle \frac{1}{x\ln a}}$.

Proof

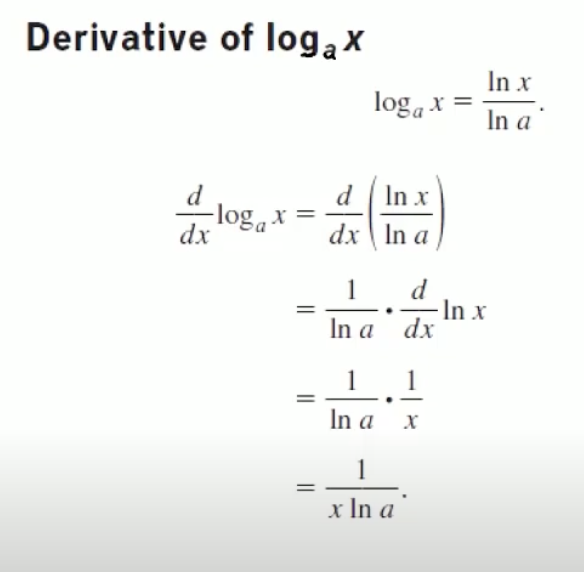
Any general ${\log }_{a}u$

• More chaining.
  ${\displaystyle \frac{d}{dx}({\log }_{a}u)=\frac{1}{u\ln a}\left(\frac{du}{dx}\right)}$

Logarithmic differentiation

• Nothing major – just keep in mind that to differentiate certain equations, you may need to take the $\ln$ of both sides.

Example

Turn the equation $y=x^x$ into $\ln y=x\ln x$ before differentiating.