4.4 - Optimization

#calc/concept

Strategies for solving max/min problems

1. Understand the problem
2. Develop a mathematical model
3. Graph the function/model you made
4. Identify the function’s critical points/endpoints
5. Solve the model
6. Interpret the solution
   The most helpful thing for me personally is to just jump in, assign a couple of variables, and make a few equations. Then I can take derivatives and such as I please.

Example problem

A rectangle is to be inscribed under one arch of the sine curve. What is the largest area that such a rectangle can have, and what dimensions give that area?

Answer: We give the points these dimensions:

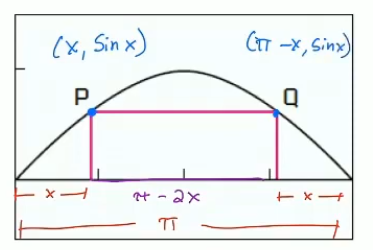
We can then use the rectangle area formula to get the equation $A(x)=\sin x(\pi -2x)$. We want to maximize this, so we take a derivative and see where $A^{\prime }(x)=0$. We find that this happens when $x=0.710$ (rounding to 3 decimal places like a good little boy) and then can plug this value of $x$ back into our original equation as we now know that the length of the rectangle $=\pi -2x=$ around $1.722$ units, and the height = $\sin x=0.652$ units. Multiply the length and width to get a final area of $1.122$.

Economics

• Economics is pretty much the same as the above; just find a model to describe whatever is happening in the problem and then take some kind of derivative or something.
  Important fact:
• Maximum profit occurs when marginal revenue is equal to marginal cost.