5.1, 5.5 - Estimating With Finite Sums, Trapezoidal Rule

We can use rectangles and trapezoids to approximate the area under a curve.

• These are not exact estimates yet, but they will be soon with Riemann sums.

LRAM, RRAM, and MRAM

• To approximate area under a curve, we can strategically place rectangles along it and take their combined area.
  • Rectangles can be placed using the left (LRAM), right (RRAM), or middle part of the top of the rectangle.
  • Worth noting: MRAM is the average

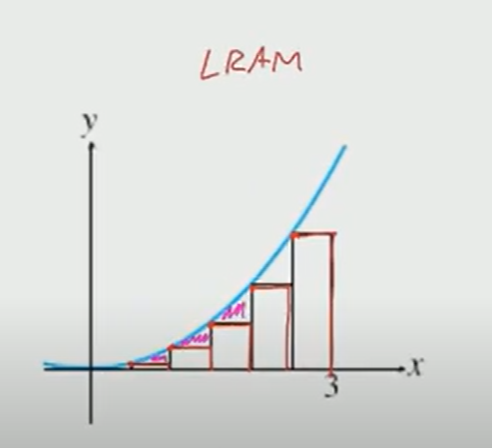
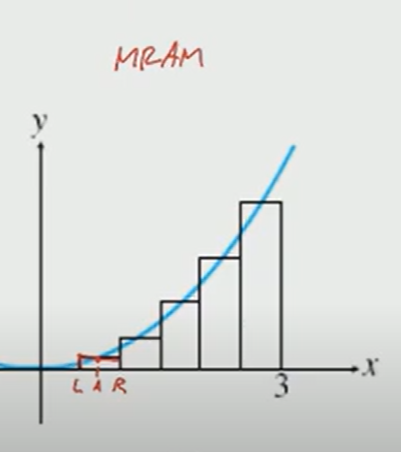
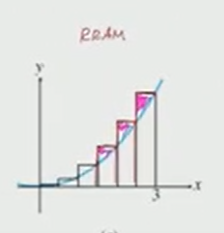
How do these measurements compare to actual area?

• For increasing functions:
  • LRAM underapproximates area under the curve
  • RRAM overapproximates
• For decreasing functions:
  • LRAM overapproximates
  • RRAM underapproximates
• Do out

Trapezoidal rule

• The same as the above, but with trapezoids!
  
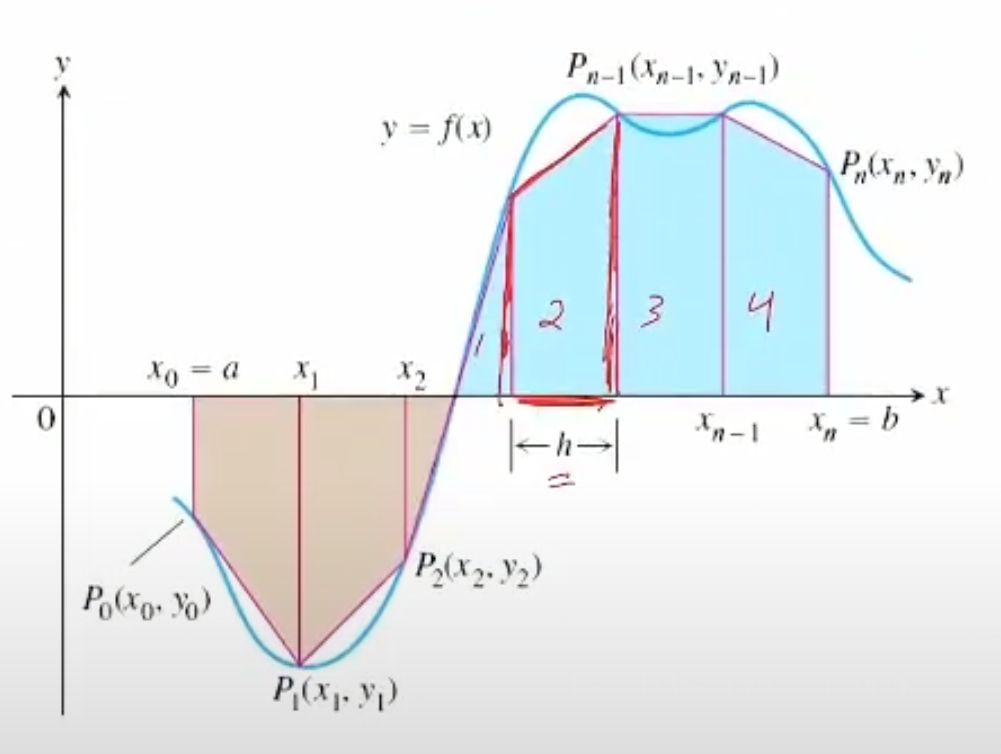
• We find the area of a trapezoid using the formula $A=\frac{1}{2}h(b_1+b_2)$.
  • Keep in mind that every trapezoid has $\frac{1}{2}h$ in common, so all we need to worry about is the bases.
• Trapezoidal rule formula: $A=\frac{1}{2}h(b_1+b_n+2(b_2+b_3+\dots ))$
• If the function is concave up, the rule is an over-estimate, and vice versa.