The Intermediate Value Theorem

#calc/theorem
A function $y=f(x)$ that is continuous on a closed interval $[a,b]$ takes on every value between $f(a)$ and $f(b)$. In other words, if $y_0$ is between $f(a)$ and $f(b)$, then $y_0=f(c)$ for some $c$ in $[a,b]$.

Stated basically

If we know that a function is continuous on an interval, we know that it passes through every single value between any two points we choose on its graph.

• This theorem is often helpful for proving that solutions exist on a given interval, and can be used in that way when you can prove the function changes from negative to positive within that interval.

Diagram

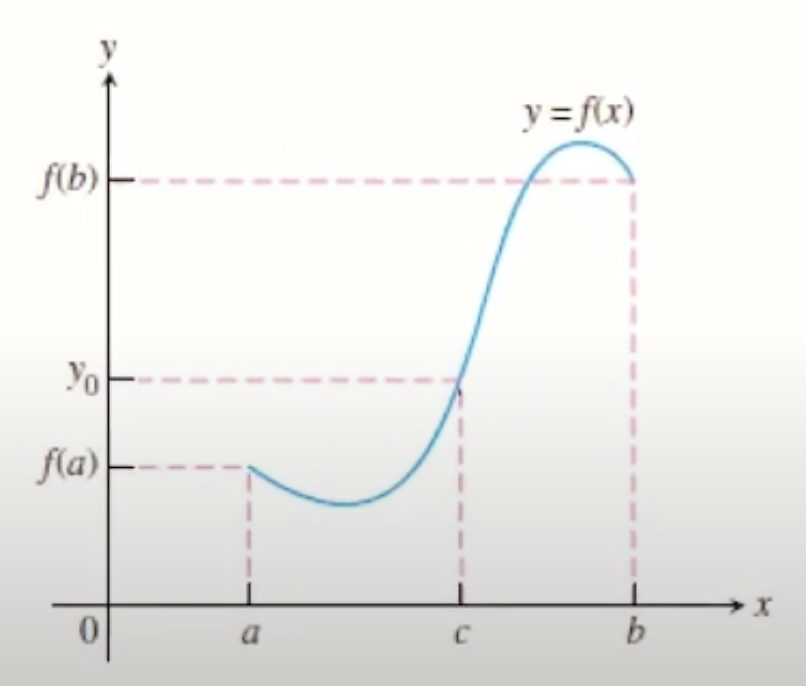
Structuring an answer using the IVT

Using the IVT on a problem involves using lots of words to structure an answer.

Example 1

Q: Does a zero of $f(x)=x^2-4$ exist on the interval $[0,3]$?
A: Since $f(x)=x^2-4$ is continuous on the given interval, the IVT applies. Because $f(0)=-4$ and $f(3)=5$, the IVT proves that $f(x)=0$ at some point on $[0,3]$.

Example 2

Q: Show that $f(x)=x^3+x-6$ has a solution.
A: Since $f(x)=x^3+x-6$ is continous on its entire domain, and $f(x)$ changes from negative to positive from $[0,10]$ , $f(x)$ must have a solution on $[0,10]$.